LA RAZÓN DE ORO EN EL ARTE

Si traducimos la proporción áurea en formas geométricas, observaremos que describe mágicamente mychas de las pautas que vemos en la naturaleza. Los arquitectos la utilizaban para crear edificios de excelente simetría. El número de oro se representa con la letra Phi (Fi), en honor al escultor griego Fidias y se trata de un número irracional.

Desde el antiguo Egipto se utiliza el numero Phi en la arquitectura. Por ejemplo en la pirámide de Keops. Si la distancia AC es igual a 1, AB mide la raíz cuadrada de phi y BC mide phi.

Del mismo modo, en la Tore Eiffel, los ejes de sus cuatro pilares forman un cuadrado de 100 metros, que seria el lado pequeño de un rectángulo áureo. Pues poniendo dos rectángulos conseguimos la altura de esta torre.

Claro, que uno de los ejemplos más bellos es el del Partenón de Atenas.

En el presente video, podemos observar la justificación matemática y la relación estrecha con la Naturaleza.

LA RAZÓN DE ORO

El número áureo (también llamado número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) es un número irracional, representado por la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula) en honor al escultor griego Fidias.

La ecuación se expresa de la siguiente manera:

El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total a+bes al segmento más largo a, como aes al segmento más corto b.

También se representa con la letra griega Tau (Τ τ),⁴ por ser la primera letra de la raíz griega τομή, que significa acortar, aunque es más común encontrarlo representado con la letra fi (phi) (Φ,φ). También se representa con la letra griega alpha minúscula.⁵

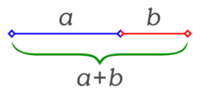
Se trata de un número algebraico irracional (su representación decimal no tiene período) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta, es decir, una construcción geométrica. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc. Una de sus propiedades aritméticas más curiosas es que su cuadrado (Φ² = 2,61803398874988...) y su inverso (1/Φ = 0,61803398874988...) tienen las mismas infinitas cifras decimales.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

CLASIFICACIÓN DE LOS NÚMEROS

Los números se clasifican en cinco tipos principales: números naturales “N“, números enteros “Z”, números racionales “Q”, números reales “R” (incluyen a los irracionales) y números complejos “C”.

• Los Números Naturales “N” son todos los números mayores de cero* (algunos autores incluyen también el 0) que sirven para contar. No pueden tener parte decimal, fraccionaria, ni imaginaria. N = [1, 2 , 3, 4, 5…]

• Los Números Enteros “Z” incluye al conjunto de los números naturales, al cero* y a sus opuestos (los números negativos). Es decir: Z = […-2, -1, 0, 1, 2…]

• Los Números Racionales “Q” son aquellos que pueden expresarse como una fracción de dos números enteros. Por ejemplo: Q = [¼, ¾, etc.]

• Los Números Reales “R” se definen como todos los números que pueden expresarse en una línea continua, por tanto incluye a los conjuntos anteriores y además a los números irracionales como el número “∏” y “e“.

• Los Números Complejos “C” incluye todos los números anteriores más el número imaginario “i“. C = [N, Z, Q, R, I]

SISTEMAS DE NUMERACIÓN

Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.

donde:

•  es el sistema de numeración considerado (p.ej. decimal, binario, etc.).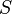
•  es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son {0,1,...9,A,B,C,D,E,F}.
•  son las reglas que nos indican qué números y qué operaciones son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.

NUMERACIÓN EGIPCIA

El sistema de numeración egipcio permitía representar números, desde el uno hasta millones, desde el inicio del uso de la escritura jeroglíficos. A principios del tercer milenio a.C. los egipcios disponían del primer sistema desarrollado decimal (numeración de base 10). Aunque no era un sistema posicional, permitía el uso de grandes números y también describir pequeñas cantidades en forma de fracciones unitarias: las fracciones del Ojo de Horus. Las cantidades se representaban de una forma muy larga. Éste es uno de los sistemas de numeración más antiguos.

NUMERACIÓN MAYA

Los mayas utilizaban un sistema de numeración vigesimal (de base 20) de raíz mixta, similar al de otras civilizaciones mesoamericanas.

Los mayas pre clásicos desarrollaron independientemente el concepto de cero alrededor del año 36 a. C. Este es el primer uso documentado del cero en América, aunque con algunas peculiaridades que le privaron de posibilidad operatoria. Las inscripciones los muestran en ocasiones trabajando con sumas de hasta cientos de millones y fechas tan extensas que tomaba varias líneas el poder representarlas.

NUMERACIÓN ARÁBIGA O DECIMAL

El sistema numérico que usamos todos los días, basado en 10 dígitos (0,1,2,3,4,5,6,7,8,9). La posición es importante, siendo la primera posición (a la derecha) la de las unidades, la siguiente a la izquierda la de las decenas, luego las centenas y y así en adelante.

NUMERACIÓN BINARIO

El sistema de numeración binario utiliza sólo dos dígitos, el cero (0) y el uno (1).

En una cifra binaria, cada dígito tiene distinto valor dependiendo de la posición que ocupe. El valor de cada posición es el de una potencia de base 2, elevada a un exponente igual a la posición del dígito menos uno. Se puede observar que, tal y como ocurría con el sistema decimal, la base de la potencia coincide con la cantidad de dígitos utilizados (2) para representar los números.

NUMERACIÓN OCTAL

El sistema numérico en base 8 se llama octal y utiliza los dígitos 0 a 7. Los números octales pueden construirse a partir de números binarios agrupando cada tres dígitos consecutivos de estos últimos (de derecha a izquierda) y obteniendo su valor decimal.

NUMERACIÓN HEXADECIMAL 

Los números hexadecimales son interesantes. ¡Hay 16 dígitos diferentes! Son como los decimales hasta el 9, pero después hay letras ("A',"B","C","D","E","F") para los valores de 10 a 15. Así que con una sola cifra hexadecimal se pueden dar 16 valores diferentes en lugar de los 10 de siempre:

Decimal:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Hexadecimal:	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

COMO SE MULTIPLICA UTILIZANDO GEOMETRÍA?

MULTIPLICACIÓN GEOMÉTRICA 

Este método que no requiere ninguna tabla de multiplicar ni siquiera escribir número alguno, sino sólo dibujar.Tomamos los números que deseamos multiplicar. En este caso,utilizaré 23 × 16 trazamos una línea paralela por cada dígito del primer número (2 y 3), dejando un buen espacio entre las correspondientes a cada dígito.

23 x 16

En este caso, nos quedan dos líneas separadas de otras tres, que corresponden al 23 de la ecuación. Luego, descomponemos del mismo modo el siguiente número (16), pero de forma perpendicular a las líneas previas.

23 x 16

Habremos agregado una línea y seis líneas más, esta vez, desde abajo hacia arriba, pero siempre de izquierda a derecha. Ahora contaremos los puntos agrupándolos verticalmente.

Finalmente, sólo hay que sumar esas cantidades de puntos alineando el último dígito de cada nuevo número un lugar después del último del número anterior. Ni siquiera hace falta que lo pienses; sólo mira el gráfico. La gracia de este método es que no requiere pensar, así que no lo arruinaré con explicaciones (tiene que ver con las centenas, decenas y unidades). Debe quedar una escalera que se baje de izquierda a derecha.

20015018

  2 

+15

       18

-------------

368

En efecto, 23 x 16 = 368